ģ���� ��������
����6. һ��Բ���ܵ��� 500 ��, �ס� �����˴Ӳ�ͬ���ͬʱ����, ����˳ʱ�뷽�������ܲ��� ��֪������ 600 ���һ������, �˺���� 20%����ǰ��, ������ 1200��ڶ������ҡ� �ʼ׳����������һ�ε����ҵij�����?
����A. 100
����B. 120
����C. 150
����D. 180
����7. ����Ϊ�ס� ������֮����ٹ�·�ϵ�һ�����ٵ�, �����֮��ľ��������ҵ�֮������һ��, A�� B �����ֱ�Ӽغ��ҵ�ͬʱ���������������, ��һ��ӭ��������λ�þ������ 500 ��, ��������Է������غ�����ԭ·����, �ڶ�����������ҲΪӭ������, �ʵڶ���������λ��һ��:
����A. ����� 1500 ��
����B. �����ҵ� 1500 ��
����C. ������� 1500 ��
����D. �����ҡ� ���е� 1500 ��
����8. �ס� �ҡ� ���������ų�Ϊ 500 �ס� ��Ϊ 250 �ij����γ����ܲ�, ������ 2: 1:3 ���ٶ�֮������˳ʱ���ܲ��� �����볡��ʱ�������� 1 / 3 Ȧ, ��������ʱ������100 �ס� �ʵ������� 2 Ȧʱ, �������λ�ù�ϵ���?
����A. �����ȼ� 3000 ��
����B. �����ȼ� 2900 ��
����C. �����ȼ� 2450 ��
����D. �����ȼ� 2350 ��
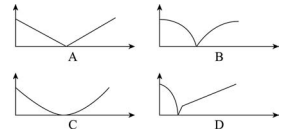
����9. �ס� ������С������� 100 �Ĺ������ͬʱ�����������, �׳��� 2 ��/ ����ٶ�������ʻ, �ҳ��Ӿ�ֹ״̬��ʼ�� 1 ��/ �� 2 �ļ��ٶȾ��ȼ�����ʻ, �����յ��ͣ�¡� �������ĸ�ͼ��ȷ�������Ҹ��Ե����յ�ǰ, ����֮��ľ�����ʱ��Ĺ�ϵ(����Ϊʱ��, ����Ϊֱ�߾���)?
����10. A�� B ������� 600 ǧ��, �׳����� 9 ʱ�� A �ؿ��� B ��, �ҳ����� 10 ʱ�� B�ؿ��� A ��, ������ 13 ʱ, ������ǡ���� A�� B ���ص��е������� ����ס� ���������������� 9 ʱ����������, �ٶȲ���, ������ 11 ʱ, ������������ǧ��?
����A. 100
����B. 150
����C. 200
����D. 250
����11. һ���ִ�˳������, �Ӽص��ҵ���Ҫ 6 ��; ��������, ���ҵص�����Ҫ 8�졣 ����������������, һ��Ư��ƿ�Ӽص��ҵ���Ҫ������?
����A. 24
����B. 36
����C. 48
����D. 56
����12. �ס� ��������һ�� 400 �Ļ����ܵ��ϴ���� 200 ��λ�ó���, ͬ�������ܲ��� �����������ҵ�ʱ��, ������ 2000 �ס� �ʼ��ٶ����ҵĶ��ٱ�?
����A. 1. 2
����B. 1. 5
����C. 1. 6
����D. 2. 0
ɨ�롾���ӿͷ���������ȡ��ͼ�ο���
